Muitas vezes pensamos que a Matematica é algo complicado e fora de nossa realidade, mas na verdade isso não ocorre. A matematica é mais proxima de nós do que imaginamos. Pense como seria se voce vivesse em um lugar que não conhecesse o conceito de números. Como voce faria para quantificar e comparar unidades e medidas? Imagine um local sem o conhecimento das figuras geometricas. Como voce conseguiria, por exemplo, construir sua casa?
É justamente pensando nestas situações que vamos começar a estudar um pouco sobre figuras geometricas e começaremos pela figura mais antiga, o TRIANGULO.
Triangulo
Mas como surgiu e quem descobriu essa figura?
O conceito de triangulo é tão antigo quanto os primeiros estudos de matematica. Provavelmente surgiu atraves de uma observação.
Em Geometria não se pode obter uma figura totalmente perfeita, nem com uma, nem com duas linhas retas. Mas três linhas retas em conjunção produzem um triângulo, a figura absolutamente perfeita.
Classificação dos triangulos
Os triangulos podem ser classifcados observando-se os lados e os angulos.
Com relação a observação das medidas dos lados podemos dizer que um triangulo:
É equilatero quando tem os tres lados de mesma medida.
É isósceles quando possuir dois lados de medidas iguais e um lado de medida diferente dos demais.
É escaleno quando possuir todos os lados de medidas diferentes.
Classificação dos triangulos quanto aos lados
Com relação a observação das medidas dos angulos, podemos dizer que um triangulo:
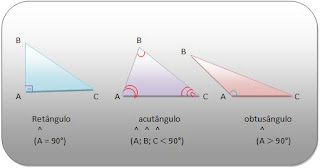
É acutangulo quando todos os angulos internos medem menos de 90º.
É retangulo quando um de seus angulos internos medir 90º.
É obtusangulo quando um de seus angulos medir mais de 90º.
Classificação dos triangulos quanto aos angulos
Soma dos angulos interno de um triangulo
Estamos acostumados a ouvir
"A soma de todos os angulos internos de um triangulo é 180º "
Mas o que realmente significa isso? Como podemos ter certeza desta afirmação?
Primeiro precisamos entender o que significa 180º. Um instrumento que é usado para medir angulos chama-se transferidor. Olhando para ele podemos então perceber que uma semireta tem angulo de 180º.
Exemplo de transferidor
Assim podemos representar um angulo de 180º como a figura abaixo
Agora podemos então entender porque podemos afirmar que a soma dos angulos internos de um triangulo é 180º. Para visualizarmos esta afirmação faça um triangulo qualquer de papel, pinte cada angulo interno deste triangulo e recorte o triangulo nas linhas pontilhadas como na gravura abaixo
Em seguida junte os angulos e observe a figura que irá formar.
Entendeu o que a afirmação nos diz?
RESUMINDO







Nenhum comentário:
Postar um comentário